Euclides, el padre de la geometría
/
Una de las obras que desde la antigüedad mostraron a la humanidad las reglas de esta rama de las matemáticas es los Elementos de Euclides, primer tratado que definió conceptos hoy usuales pero necesarios para la vida diaria
/
POR RAÚL ROJAS
Dicen que el futbol es el ballet de las masas. Pues entonces la obra de matemáticas más célebre de la historia, los Elementos, escrita por el legendario Euclides de Alejandría, constituye la ópera, el concierto y el ballet de los científicos. Es el ejemplo más antiguo, pero aun así más acabado, de cómo aplicar el método axiomático para deducir verdades matemáticas. Los trece libros de los Elementos albergan una cantidad enorme de demostraciones geométricas. Éstas van desde las construcciones planas, con regla y compás, hasta la consideración de figuras tridimensionales, como son el cubo, la esfera o el dodecaedro. Desgraciadamente, hoy en día ni los matemáticos leen una porción significativa de los Elementos. Desde que se introdujeron métodos algebraicos en la geometría, gran cantidad de problemas se pueden resolver más rápidamente realizando cálculos simbólicos. Aún así, repasar las demostraciones de Euclides es una oportunidad intelectual que ningún estudiante de ciencias o de ingeniería debería dejar pasar.
Durante siglos se ha discutido si Euclides realmente existió, ya que los Elementos bien podrían representar un esfuerzo de un grupo de matemáticos griegos confabulados para producir una obra colectiva. No poseemos ninguna primera edición, por así decirlo, sino sólo copias caligráficas de siglos posteriores. La fecha precisa de su creación no se conoce, pero generalmente se piensa que podría haber sido escrita en el siglo tercero antes de nuestra era, es decir, hace casi 2 mil 300 años. Se sigue imprimiendo, a pesar de los años transcurridos. De hecho, durante muchos siglos el estudio de la geometría euclidiana perteneció al canon académico de las universidades europeas. El mismo Isaac Newton, inventor del cálculo diferencial e integral, prefirió no utilizar los nacientes métodos algebraicos sino presentar su teoría de la gravitación utilizando los métodos de exposición de Euclides, para así lograr mejor aceptación.
En los Elementos se parte de una lista mínima de definiciones, como, por ejemplo, decir que el punto es aquello que no tiene partes, o que una línea es una longitud sin grosor. Un círculo se define como todos aquellos puntos con la misma distancia a un punto fijo, llamado el centro. Habiendo definido los objetos geométricos que se quiere investigar (como si fueran las piezas de un Lego matemático), hay que definir las relaciones entre esos componentes y las operaciones permitidas con la regla y el compás. Es así que Euclides formula cinco axiomas, los que en aquella época se consideraban simplemente como verdades tan evidentes que no requerían demostración alguna. El primer axioma, por ejemplo, afirma que dos puntos determinan un segmento de línea recta. El segundo axioma establece que un segmento se puede extender hacia el infinito, como línea. El quinto axioma es el llamado axioma de las paralelas, al que regreso más abajo.
Dados los axiomas y aquellas reglas que se deben seguir para poder combinar construcciones geométricas, hay que avanzar paso a paso. Se utiliza la pura lógica para derivar nuevas verdades (los teoremas) de otras verdades ya aceptadas. En los Elementos, la primera proposición que se demuestra es la siguiente: dado un segmento cualquiera, se puede construir un triángulo con tres lados iguales a ese segmento. La demostración utiliza un diagrama, de regla y compás, y anotaciones con letras que se refieren a puntos o bien líneas del diagrama. La argumentación es puramente verbal, refiriéndose a teoremas ya demostrados que, entretejidos con los axiomas, hacen posible verificar el nuevo teorema. Por ejemplo, la segunda proposición sólo afirma que un segmento dado se puede desplazar (copiar) a cualquier otra parte del plano. La tercera proposición muestra que, dados dos segmentos de longitud diferente, el más pequeño se puede incrustar como parte del más largo. Y así sucesivamente, a lo largo de los 13 libros, que en mi edición inglesa de la obra representan unas 400 páginas.
Es difícil saber, a menos que sea uno mate-arqueólogo, si los Elementos que se editan hoy en día no han simplificado la notación y el lenguaje para hacer la obra más accesible. El fragmento más arcaico de los Elementos que ha sido preservado es un papiro elaborado doscientos años después de Euclides. El manuscrito completo más antiguo de los Elementos está alojado en la Biblioteca Bodleiana de la Universidad de Oxford y data del año 888 de nuestra era, es decir, casi once siglos después de Euclides. Esa copia de Oxford contiene dos libros adicionales que normalmente no se consideran parte de los Elementos por ser extensiones muy posteriores.
Pero aun si algunas versiones han sido maquilladas para beneficio de los lectores de la era moderna, es posible apreciar la forma en que se hacía matemáticas en los tiempos de Euclides. En los Elementos no está presente una notación matemática propiamente dicha, sólo hay referencias verbales a los símbolos que representan puntos, líneas o círculos. Toda la argumentación es platicadita y en vez de escribir “A=B”, se dice: “el elemento A es igual al elemento B”, con todas sus letras. Esto es lo que se ha llamado las “matemáticas retóricas”, que prescinden de los símbolos que hoy en día conocemos. Se requiere leer muy atentamente para no perderse al seguir argumentaciones puramente discursivas.
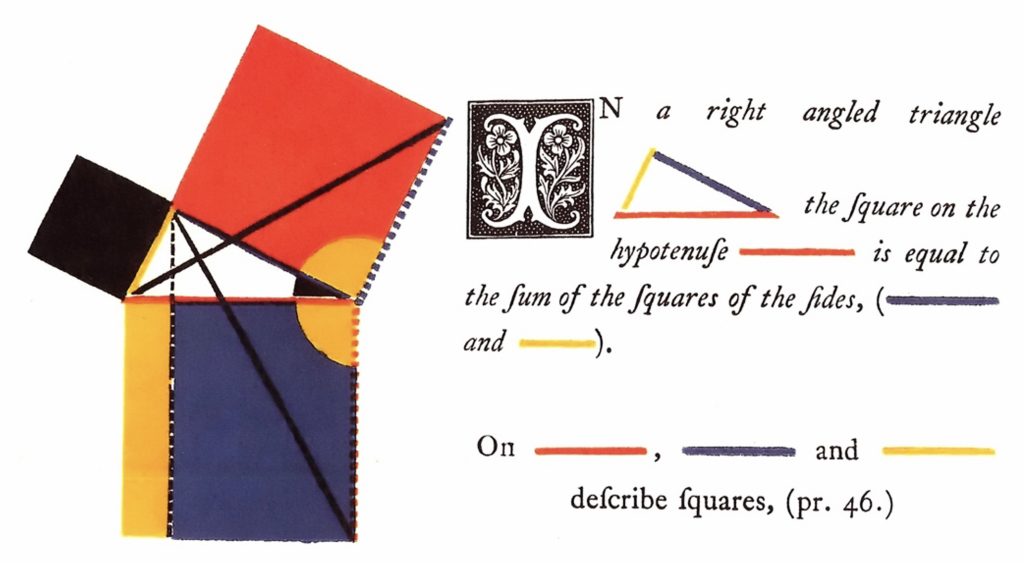
Mi edición favorita de los Elementos es la publicada en 1847 por el matemático irlandés Oliver Byrne, aunque sólo abarca los primeros seis libros. Byrne tuvo una idea genial. Ya que en los diagramas de Euclides a veces es difícil reconocer qué segmentos son iguales, o qué ángulos son congruentes, lo que hizo Byrne fue redibujar todos los diagramas, pero utilizando colores. Con ello, la igualdad de segmentos, ángulos o componentes geométricos salta a la vista y es mucho más fácil seguir la demostración matemática, ya que Byrne integra además los símbolos modernos de igualdad, adición, etc. Es posible avanzar más rápido en la lectura, que se convierte, además, en un verdadero festejo sensorial e intelectual.
Examinando las diversas secciones de los Elementos, lo que más me sorprende es todo lo que se puede demostrar con regla y compás, a veces más rápido que utilizando métodos algebraicos. Que un círculo puede intersectar a otro círculo, en un máximo de dos puntos, ya se demuestra en las primeras páginas. Un teorema nada trivial aparece ya al principio del tercer libro: dados dos puntos fijos, el vértice de un ángulo constante describe un círculo, si cada uno de sus dos lados está en contacto siempre con uno de los puntos fijos.
El primer gran desafío a la geometría euclidiana fue el descubrimiento de geometrías donde el axioma de las paralelas (“por un punto externo a una línea se puede trazar una y sólo una línea que no intersecta a la primera”) no se aplica. Si en vez de utilizar el plano utilizamos la superficie de una esfera para investigar su geometría, de pronto los axiomas de Euclides sólo son válidos si las líneas las concebimos ahora como círculos “máximos” (es decir de máximo perímetro). Pero ahora todas las líneas se intersectan, necesariamente, y no existen líneas paralelas entre sí. Esto es lo que se llama la “geometría esférica”, la que fue propuesta posteriormente a la llamada “geometría hiperbólica”, en donde por cada punto externo a una línea pueden trazarse un número infinito de líneas paralelas. En el siglo XIX el húngaro János Bolyai y el ruso Nikola Lobachevsky publicaron sus ideas sobre geometría hiperbólica, sólo para descubrir que el gran Carl Friedrich Gauss ya había estado ahí. Hoy en día en la cosmología se discute si nuestro universo posee, en gran escala, una geometría euclidiana, esférica o hiperbólica. Hasta ahora lleva la delantera Euclides y se dice que el universo seguirá expandiéndose eternamente y que además es “plano” (es decir, euclidiano).
Precisamente para dilucidar la geometría del universo, la Agencia Espacial Europea (AEE) está por lanzar en 2022 el satélite “Euclides”. La sonda, que será puesta en órbita desde Guyana, va repleta de sensores con los que se puede evaluar el espectro de las galaxias más lejanas con mucho mayor precisión que desde la tierra. Se podrá también observar el surgimiento de las estructuras cósmicas. Con esas mediciones se puede determinar la velocidad de expansión del universo, para así determinar si corresponde a un universo con geometría euclidiana, esférica o hiperbólica. Del nombre de la sonda parecería que la AEE espera que se confirmen las mediciones hasta ahora realizadas, pero con mayor precisión.
A partir de mediados del siglo XIX llegó la era del rigor en las matemáticas. Todo aquello que era tácitamente “aparente” y no requería demostración tuvo que ser especificado de otra manera. El matemático alemán David Hilbert puso de manifiesto todos los supuestos implícitos que se utilizan en los Elementos con su fabuloso libro Fundamentos de la Geometría. En vez de definir al punto, la línea y otros objetos geométricos, Hilbert los declara “conceptos indefinidos”, cuyo significado estará dada por sus relaciones mutuas. Hilbert muestra que, al avanzar poco a poco, agregando un axioma tras otro, se puede abarcar sucesivamente a diversas geometrías, desde aquellas con un número finito de puntos, hasta geometrías continuas, pero con propiedades inusitadas. Para cualquiera que se ha esforzado alguna vez en leer a Euclides, el libro de Hilbert resulta una revelación.
En cierto modo, Hilbert quería extender y terminar el programa de Euclides. Para Hilbert las matemáticas deberían ser “completas” y libres de contradicciones, como trató de lograr con sus Fundamentos para el caso de la geometría. Sería fatal erigir un edificio teórico enorme sólo para encontrar que los teoremas se contradicen. Además, cualquier verdad matemática debería tener una demostración. Hoy sabemos que las cosas son mucho más complicadas, por cortesía de Kurt Gödel y el famoso teorema que lleva su nombre. Pero David Hilbert estaba tan seguro de que las matemáticas eran completas y libres de contradicciones, que alguna vez afirmó: “Debemos saber; vamos a saber”. Esa contundente frase decora la lápida de su tumba en Gotinga.
Los Elementos concluyen investigando lo que ahora se llama los sólidos platónicos, es decir los poliedros que tienen caras poligonales idénticas, ya sean triangulares, cuadradas o pentagonales. Históricamente la obra es el punto de partida de las matemáticas basadas en demostraciones que se rigen puntualmente por el método axiomático. El tratado de Euclides representa por ello la alborada de esta disciplina: antes de Euclides teníamos conocimiento pre matemático, después de los Elementos comienza la era de la verdad matemática.
FOTO: Euclides fue representado con un compás en la mano en La escuela de Atenas, de Rafael, que se encuentra en el Palacio Apostólico del Vaticano./Especial
« Descifrar a Mussolini. Entrevista con Antonio Scurati Sara Mesa: “El machismo es una forma de tomar el poder” »